Wraz z rozwojem zastosowania teorii gier w różnych dziedzinach zarówno nauki jak i życia przyszła kolej na aspekty biologiczne, a w szczególności problem doboru naturalnego. Proste rozumowanie jak i obserwacje wykazują, że w sytuacjach kiedy dany osobnik wygrywa w walce np. o ograniczone zasoby, pokarm, miejsce na gniazdo, samice czy terytorium, powinien zostawić w przyszłych pokoleniach więcej swego materiału genetycznego, niż osobnik, który przegrał rywalizację. W dodatku często, przynajmniej początkowo uważano, że to zachowanie, czy też strategie agresywne są tymi promowanymi decyzjami. Zatem tendencja do ustępowania jak i tendencja walki aż do wygranej lub do śmierci są genetycznie zdeterminowane, wówczas należy się spodziewać, że część z tych zachowań, jak walka nie na serio (pewne zachowanie zrytualizowane), czy ustępowanie, powinny zostać dawno wyparte i wyeliminowane przez dobór. Co więcej, jeżeli akceptujemy ten fakt, wówczas przyjmujemy, że takie zachowania jak ustępowanie czy pewien zrytualizowany konflikt (jak konkurowanie poprzez straszenie się przy walkach godowych, walkach o terytorium czy ustalanie przewodnictwa w grupie) nie mogą pojawić się drogą doboru naturalnego, tylko w jakiś inny sposób. Jest to związane z tym, że takie osobniki zostawiają mniej materiału genetycznego przyszłym pokoleniom, dlatego też ich zachowanie nie jest kultywowane przez potomstwo. Konrad Lorenz w swych książkach sugerował, że takie zachowanie pozostaje w populacji, ponieważ jest dobre dla całego gatunku i zapobiega nadmiernej śmiertelności w wyniku agresji. Zarówno rozumowanie Konrada Lorenza jak i wielu innych biologów nie jest w żaden sposób tłumaczone przez mechanizm doboru. Takie zachowania bowiem teoretycznie prowadzą do cech dobrych dla jednostki, dla osobnika, a nie dla całego gatunku. W świetle darwinowskiej teorii doboru naturalnego takie zachowania jak ustępowanie albo walki konwencjonalne są niezrozumiałe, a neodarwinizm z genetyką populacyjną też tych zjawisk nie tłumaczył. Zatem problem dalej istniał i należało znaleźć uzasadnienie na poziomie interakcji pojedynczego osobnika jak i całej populacji, czy poszczególnej grupy wykazującej tendencje do tych samych zachowań.
      
Tego typu problem zainspirował Johna Maynarda Smitha do wykorzystania wcześniej opisanej teorii gier w celu wyjaśnienia tego biologicznego zjawiska. W ten sposób narodziła się nowa dziedzina nauki – teoria gier ewolucyjnych, mająca na celu badanie zjawisk, których ograniczona do racjonalizmu i bezgranicznej wiedzy graczy klasyczna teoria gier nie może określić. Dlatego też, o czym wyżej było wspominane, ewolucyjne teorie gier są rezultatem spotkania się dwóch naprawdę potężnych dziedzin nauki, które posiadają sowity dorobek. Należy tu jeszcze wspomnieć o prawdziwym sprzężeniu zwrotnym, bowiem metody stworzone na potrzeby biologii (odnoszenie się do populacji, brak racjonalności oraz wszechwiedzy) wróciły do ekonomii, gdzie są licznie wykorzystywane.
   
    W grach ewolucyjnych strategie odpowiadają zbiorowi dziedziczonych cech danego osobnika. Są te pewne zakodowane zachowania jak i instynkt, które nie podlegają racjonalnemu osądowi. Gracze są częścią populacji, w obrębie której dochodzi do interakcji między nimi, czego efektem jest zwiększenie (lub zmniejszenie) szansy na przekazanie swoich genów następnemu pokoleniu. W wyniku różnic w dostosowaniu danego osobnika do środowiska w danej populacji liczba potomstwa, a tym samym liczby osobników wykazujących odpowiednie strategie przetrwania w populacji będą ulegać zmianie. Wyniki mogą być różne: od wyparcia pewnych cech i zachowań z populacji po osiągnięcie ustalonych, stabilnych wartości np. w całkiem innych proporcjach niż to było początkowo. Ale właśnie w ten sposób działa proces ewolucyjny odpowiadający za zmiany dochodzące w obrębie gatunku na przestrzeni nowych pokoleń i generacji, jak i zmian w otoczeniu, w którym znajduje się dana populacja.

Papier, nożyce, kamień
    Papier, nożyce, kamień to gra znana każdemu z dzieciństwa. Pozwala w prosty sposób rozwiązywać różne spory i konflikty. W tym modelu mamy trzy strategie i w skrócie mówiąc każda może prowadzić do wygranej bądź przegranej. Mianowicie kamień wygrywa z nożycami, nożyce z papierem, a papier z kamieniem.
   Jest to także model teoriogrowy, który znalazł swoje odniesienie również w biologii. Ten typ relacji pomiędzy każdym z graczy i jego strategiami występuje wśród różnych fenotypów samców jaszczurek Uta stansburiana występujących w Kalifornii. Opisał to Maynard Smith w 1996 w artykule The games lizards play. W owej populacji występują trzy motywy zachowań odnośnie samic, co można odróżnić po kolorze plam u samców na podgardlu. Agresywne samce pomarańczowe starają się zdobyć jak największą ilość samic i skutecznie odganiają inne samce. Ale mogą być łatwo oszukane przez samce żółte, podobne do samic i niewywołujące agresji. Wykorzystują one fakt, że samce pomarańczowe nie są w stanie upilnować wszystkich samic. Zatem samce żółte mają przewagę nad pomarańczowymi. Niestety są jeszcze samce niebieskie, które są dość wierne i nie pozwalają podkraść się samcom żółtym. Z drugiej strony samce niebieskie są podatne na agresje samców pomarańczowych.

Jastrząb i Gołąb
    Jest to jeden z prostszych i pierwszych przykładów zastosowania teorii gier ewolucyjnych. W pewnej populacji dochodzi do spotkań między osobnikami, a tym samym konfliktów: o terytorium, pożywienie czy po prostu o partnerkę. Na drodze ewolucji wytworzyły się dwa podejścia do rozwiązywania konfliktów: agresywne i ustępujące. Te dwie strategię obrazowo określa się jako strategie jastrzębia i gołębia, ale model raczej odnosimy do populacji osobników tego samego gatunku:

• strategia jastrzębia (agresywna) – nie wycofuje się z pola walki niezależnie od kosztów czy obrażeń jakie może ponieść.

• strategia gołębia (ustępującego) – kiedy jest możliwość doznania jakichkolwiek obrażeń po prostu ustępuje.

Strategie oraz ich wypłaty można zapisać następująco:

Symbole użyte w tabeli to:
W – zysk z wygranego (nieważne w jaki sposób) konfliktu
K – koszt, straty, rany poniesione podczas konfliktu (nie koniecznie oznaczają przegraną walkę).
Podobnie jak w przypadku dylematu więźnia, wypłata zależy od wyboru strategii a nie od osobnika, który ową strategią się posługuje (tj. każdy jastrząb jest tak samo silny).

    Jeżeli jastrząb spotka jastrzębia wartość oczekiwana konfliktu wyniesie (W-K)/2. Jeżeli jastrząb spotka gołębia, czyli jednostkę ustępującą, otrzymuje pełne zyski W, w sytuacji odwrotnej osobniki łagodne zawsze uciekają nie ponosząc ani strat ani zysków. W przypadku spotkania gołąb-gołąb wypłata jest uśredniona i wynosi W/2, bowiem jest 50% szansy, że przeciwnik wystraszy się i ucieknie .
    Jeżeli zyski z wygranej są większe od potencjalnych strat (W>K), wtedy zawsze najlepszym wyborem jest strategia jastrzębia, to znaczy, że osobnik będący gołębiem zawsze jest gorzej dostosowany (ma mniejszą wypłatę) niż osobnik będący jastrzębiem, Czyli nawet jeśli w populacji pojawią się gołębie (na drodze mutacji czy migracji osobników) to zawsze zostaną wyparte z niej przez jastrzębie.
    W przypadku kiedy zyski z wygranej nie rekompensują strat (W<K) wtedy strategia gołębia bardziej się opłaca przy spotkaniu z jastrzębiem niż jastrzębia z jastrzębiem (lepiej uniknąć walki niż ponieść straty). Jednakże kiedy jastrząb spotyka gołębia wtedy dalej zyski z tej rywalizacji są większe niż w przypadku spotkania gołębia z gołębiem. Nie ma tutaj zatem strategii, która w 100% dawałaby zawsze wygraną. Dlatego należy rozważyć sytuację kiedy gracz może posługiwać się daną strategią z pewnym prawdopodobieństwem. W obliczu gier ewolucyjnych oraz zastosowania teorii gier do modelowania zachowań osobników w populacjach prawdopodobieństwo to możemy odnieść do prawdopodobieństwa spotkania osobnika posługującego się daną strategią. Prawdopodobieństwo to możemy obliczyć ze zestawienia wartości średnich dostosowań (wypłat) dla danej strategii. Suma prawdopodobieństw napotkania danego osobnika w populacji musi być równa 100%, czyli możemy założyć, że ilość jastrzębi to x, natomiast gołębi to 100%-x. Średnie przystosowania liczymy z macierzy wypłat (czytając pionowo) dla każdej strategii: dla jastrzębia będzie to suma prawdopodobieństwa napotkania jastrzębia x wymnożonego przez (W-K)/2 oraz prawdopodobieństwa napotkania gołębia 100%-x wymnożonego przez W; analogicznie postępujemy dla gołębi.

W ten sposób otrzymujemy następujące równanie:
x*(W-K)/2 + (100-x)*W = x *0 + (100-x)*W/2
Po prostych przekształceniach uzyskujemy:
x=W/K*100
   
    Jeżeli zyski z walki są większe niż koszty (pierwszy analizowany przypadek), wtedy jastrzębie niepodzielnie rządzą w populacji, tj. prawdopodobieństwo ich napotkania wynosi 100%,
    Jeżeli zyski z walki są mniejsze niż koszty (drugi analizowany przypadek), wtedy populacja jest podzielona pomiędzy obie strategie, np. zakładając W równe 3, a K równe 4 mamy populacje składającą się w 75% z jastrzębi i 25% z gołębi.
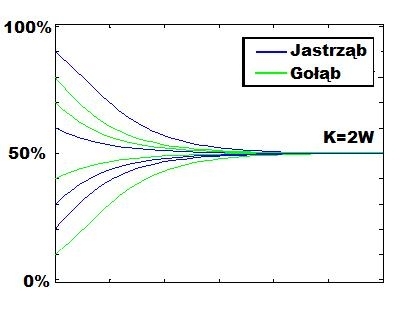
    W pierwszym przypadku mamy do czynienia ze strategią ewolucyjnie stabilną, w drugim natomiast ze stanem ewolucyjnie stabilnym. Zarówno strategia jak i stan ewolucyjnie stabilny powodują, że nawet jeśli w populacji dojdzie do gwałtownych zmian (migracje osobników, kataklizmy itp.) to po pewnym czasie stan populacji powróci do pierwotnego.
   
    Model ten pokazuje, że dwa zupełnie różne zachowania mogą utrzymać się w populacji. Co więcej, pomimo jego prostoty odzwierciedla on wiele zachowań i zjawisk występujących w przyrodzie. Głównie chodzi o fakt istnienia rytualnych zachowań (nawet wśród gatunków dobrze uzbrojonych jak drapieżnicy) w rozwiązywaniu konfliktów, a brak walk na śmierć i życie, które doprowadziłyby do wyniszczenia i przyniesienia strat w kontekście całej populacji i gatunku.

Teoria gier a komórki nowotworowe
    Teoria gier ewolucyjnych również została zastosowana w modelowaniu zjawisk nowotworowych. W nowotworze istnieją komórki, które posiadają różne cechy i właściwości.  Przykładowo, część z nich potrafi produkować czynniki wzrostu, część potrafi stymulować nasz organizm do tworzenia naczyń krwionośnych (dostarczając tym samym tlen i substancje odżywcze) część jest w stanie dosłownie unikać śmierci (tj. nie reagować na sygnały obronne z naszego organizmu), a inne potrafią przerzutować w inne rejony organizmu.
    Teoria gier udostępnia prosty aparat pozwalający na symulowanie populacji komórek nowotworowych. W takiej populacji znajdują się komórki o różnych strategiach i teoria gier pozwala na określenie, które strategie przy jakich warunkach będą dominować w populacji i w jakim stopniu. Najprostsze modele są analogiczne do modelu jastrząb-gołąb (np. zakładają istnienie komórek zdrowych oraz nowotworowych, które produkują czynniki wzrostu), bardziej złożone zawierają więcej strategii jak i również pozwalają na symulacje przestrzennego rozłożenia komórek czy uwzględnienie wpływu środowiska (np. układu odpornościowego, albo terapii antynowotworowych).
    Jednym z ważniejszych wniosków z wykorzystania teorii gier do symulacji zmian nowotworowych jest to, że w populacjach komórek również istnieją stany ewolucyjnie stabilne. Czyli takie stany, które nawet po zmianie proporcji danych komórek w populacji wracają do poprzedniego stanu. To potwierdza obserwacje kliniczne, gdzie nawet po usunięciu nowotworów następuje jego nawrót. Teoria gier sugeruje, że najpierw warto zmienić zasady gry (dosłownie zmienić macierz wypłat opisującą grę), a następnie zmienić  proporcje graczy w populacji co doprowadzi do nowych stanów ewolucyjnie stabilnych. Symulacje pokazują też niestety, że tego typu ingerencje nie zawsze są korzystne, a linia pomiędzy stanem ewolucyjnie stabilnym korzystnym a groźnym dla organizmu może być bardzo cienka.

                                                                                                   Dr inż. Michał Krześlak